SinHub's Blog

それはどうかな

0%

浅析 SQL 中的树结构的分层存储

发表于 更新于 分类于

转眼就到了四月份，当初信誓旦旦勤更 blog 的诺言已经烟消云散(一时摸鱼一时爽，一直摸鱼一直爽)，想到这里不禁感到痛心疾首 (;´Д`) 。最近刚忙完个前端项目，转头就回头投入到另一个智能化社区的项目里头；然后又碰到了那个业务上老生常谈的问题，无论是小区楼宇的划分，还是组织的上下级关系，抑或是最常见的论坛评论引用都会出现：怎样存储一颗树？

“—— 不会吧，都 2021 年了，为什么不把树存到 JSON 里去，大把的 NoSQL 支持 JSON 结构，哪怕是关系型数据库也有一堆可选的。”诚然，使用 JSON 最大的好处就是 维护整棵树 都比较方便，但是当我们要更新树的节点、查询节点的关联关系，都不如纯关系数据库那么方便。不过既然是老生常谈的话题，集思广益一下，终会有适合自己的方法。这次就列举了四个常见的范式，所以篇幅可能略长（不过和翻译类 blog 对比可能还不算 (´_っ`) ）。

这里我们基于 MySQL 来说明，以回复评论的评论链作为例子:

评论链1

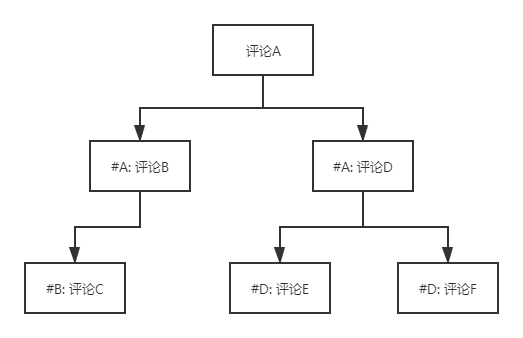
注意，虽然我这里画的树比较简单看上去像是只支持二叉树，实际上对于多叉树来说以下的方法也依然适用，并没有说只能支持二叉树。

邻接表 Adjacency List

邻接表可以说是最为简单直观的解决方案，其基本思路就是 添加 parent_id 字段，引用同一张表的其他回复 。如下所示表结构

table.sql
1
2
3
4
5
6
7
8
CREATE TABLE comments  (
  `comment_id` int(10) UNSIGNED NOT NULL AUTO_INCREMENT,
  `comment_text` varchar(255) CHARACTER SET utf8mb4 COLLATE utf8mb4_general_ci NOT NULL,
  `parent_id` int(11) UNSIGNED NULL DEFAULT NULL,
  PRIMARY KEY (`comment_id`) USING BTREE,
  INDEX `parent_id`(`parent_id`) USING BTREE,
  CONSTRAINT `FK_comments` FOREIGN KEY (`parent_id`) REFERENCES `comments` (`comment_id`) ON DELETE RESTRICT ON UPDATE RESTRICT
)

这里外键约束不是必须的，只是保证了数据的完整性。

评论链示例的表数据如下所示：

comment_id comment_text parent_id
1 A 0
2 B 1
3 C 2
4 D 1
5 E 4
6 F 4

树的维护

使用邻接表实现树形结构的好处显而易见 —— 至少在树的维护层面上：

如给树添加一个节点：

insert.sql
1
2
-- 给 F 评论添加一个引用评论 G 
INSERT INTO comments (`comment_text`, `parent_id`) VALUES ('G', 6);

修改一个节点或者子树：

update.sql
1
2
-- 将评论 F 的引用指向评论 C 
UPDATE comments SET `parent_id`=3 WHERE `comment_id`=6;

删除一个节点稍微复杂一点：如果你要删除的是子树，在不使用外键的前提下，你需要将对应子树的所有节点找出来并一一删除，否则可以使用 ON DELETE CASCADE 的外键约束自动处理这个步骤；如果你需要删除一个非叶子节点并提升其子节点，那么你需要先将其子节点的 parent_id 指向另一个节点之后再来删除这个节点。

树的查询

使用邻接表的查询远不如实现它那么简单，最起码的 查询一个节点的所有后代 这个最普遍的需求就比较棘手，如下所示:

select.sql
1
SELECT c1.*, c2.* FROM comments c1 LEFT OUTER JOIN comments c2 on c1.parent_id = c2.comment_id;

这个查询仅能满足查询两层层级关系的数据，如果有三层或以上的数据，你不得不进行更多的自联结，这不仅非常笨拙，而且当要使用聚合函数(如 COUNT() 等)的时候会变得极其困难。

当然，现在的互联网应用（大多是基于 MySQL 一套）对于关联表是相当忌讳的，你也可以选择将数据加载出来由自己在程序中重新将这棵树构建出来 —— 这也是一种办法嘛。

实际上 SQL-99 已经提供了关于递归查询的表达式规范，不过由于各个数据库的实现大同小异，目前来说 SQL Server 2005 , Oracle 11g, IBM DB2 以及 PostgreSQL 8.4 已经支持了递归查询(RECURSIVE CTE) ， 而 MySQL 也终于在 8.0 以后也实现了（不容易啊）：

cte.sql
1
2
3
4
5
WITH RECURSIVE cte AS (
    SELECT * FROM comments WHERE `parent_id`=0
    UNION ALL
    SELECT c.* FROM comments c, cte WHERE c.`comment_id`=cte.`parent_id`
) SELECT * FROM cte ORDER BY `comment_id`;

路径枚举 Path Enum

因为邻接表的一个缺点就是在树中将一个给定节点的所有祖先找出来的开销非常大，因此路径枚举的做法就是 巧妙的将其祖先信息组合成一个字符串并作为其的一个属性存储起来。

表结构如下所示：

table.sql
1
2
3
4
5
CREATE TABLE comments  (
  `comment_id` int(10) UNSIGNED NOT NULL AUTO_INCREMENT,
  `comment_text` varchar(255) CHARACTER SET utf8mb4 COLLATE utf8mb4_general_ci NOT NULL,
  `path` varchar(255) CHARACTER SET utf8mb4 COLLATE utf8mb4_general_ci NOT NULL,
)

因此我们能得到示例的表数据为：

comment_id comment_text path
1 A 1/
2 B 1/2/
3 C 1/2/3/
4 D 1/4/
5 E 1/4/5/
6 F 1/4/6/

树的查询

树的查询可以非常巧妙地利用这种结构，如我们要查找评论 F 的所有祖先评论:

ancestor.sql
1
SELECT * FROM comments c WHERE '1/4/6/' LIKE c.path || '%';

如果我们要查找某个评论的所有后代评论，也很简单，将 LIKE 两边的参数互换即可:

descendants.sql
1
2
-- 查找评论 D 的所有后代节点
SELECT * FROM comments c WHERE c.path LIKE '1/4/' || '%';

不仅查询起来非常方便，而且配合聚合函数使用起来也非常简单 —— 假如 comments 表中由 poster 一列，则可以用 COUNT 统计每个人共针对这个评论发表了多少引用评论。

树的维护

实际上路径枚举和邻接表的维护几乎如出一辙：插入一个节点只需要复制其父节点的路径再补充上自己的ID即可 —— 如果ID是后生成的，可以先插入记录再修改其 path 属性；对于修改也同样；至于删除节点的情况，需要利用查询先找出来其所有子节点再批量删除或者 UPDATE 字段 path 的字符，由于查询上比邻接表来的方便，因此也较为省事。

当然，路径枚举也并非十全十美，而这主要的问题是在维护上：

  1. 因为没有外键对数据完整性约束，所有对于 path 字段的准确性都需要有程序来进行保障，同时对于字符串的校验开销必然比使用整数要大得多；
  2. 尽管我们可以给 path 字段设置非常大的空间，但这始终存在着存储的上限，因此路径枚举也不能支持树的无限扩展

嵌套集 Nested Sets

嵌套集与路径枚举存储祖先路径的做法恰恰相反，它的解决方案是 存储子孙节点的相关信息 ，这一过程基于树的深度优先遍历(DFS)进行了巧妙的设计，部分资料会将它描述为基于左右值编码的设计：对于每一个节点，都会存储一对左右值 nlft 和 nrgt 。nlft 和 nrgt 的主要特征是：每一个节点的 nlft 都小于其子节点的 nlft；其 nrgt 都大于其子节点的 nrgt ，nlft 和 nrgt 和 comment_id 都没有直接关系。

那么如何分配节点的左右值呢？最简单的办法就是对树做一次深度优先遍历，在深入访问节点（即visit(node)） 的过程中递增的分配 nlft ，并在访问节点返回的过程中递增分配 nrgt 。以评论链为例，可以得到对应的嵌套集的树形结构为:

评论链2

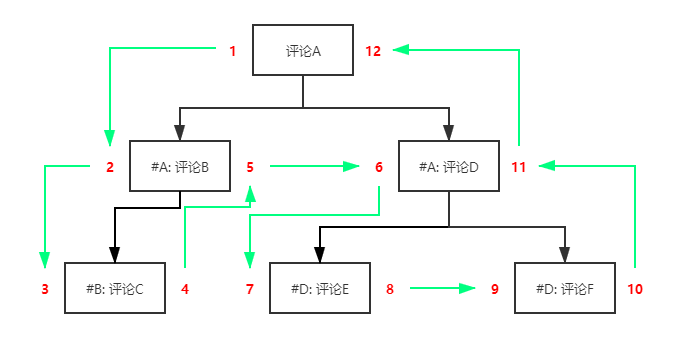
则对应的表数据为:

comment_id comment_text nlft nrgt
1 A 1 12
2 B 2 5
3 C 3 4
4 D 6 11
5 E 7 8
6 F 9 10

树的查询

基于嵌套集的特性，我们可以很方便的查找节点的祖先和后代：当我们要查找一个节点的所有后代节点，可以查找所有节点的 nlft 值大于目标节点的 nlft 值且小于目标节点的 nrgt 的集合；当我们要查找其祖先节点，只需要查找目标节点的 nlft 值位于哪些节点的 nlft 和 nrgt 值之间，则对应的节点即为其祖先节点。

descendants.sql
1
2
-- 查找评论 D 的所有后代节点
SELECT c2.* FROM comments c1 JOIN comments c2 ON c2.nlft BETWEEN c1.nlft AND c1.nrgt WHERE c1.comment_id = 4;
ancestor.sql
1
2
-- 查找评论 C 的祖先链
SELECT c2.* FROM comments c1 JOIN comments c2 ON c1.nlft BETWEEN c2.nlft AND c2.nrgt WHERE c1.comment_id = 3 ORDER BY c2.nlft;

和邻接表以及路径枚举较大的不同还在于 树的非叶子节点的删除 上。因为嵌套集实际上并不存储树的层级关系，当你删除一个非叶子节点后，其子代节点就会“自动绑定”到被删除节点的父节点上 —— 因为左右值的有序分配，而我们每次都是比较节点的相邻父兄节点，因此左右值的不连续不会对树的结构造成任何影响。

不过事情总不会一帆风顺：对于嵌套集而言，查找直接祖先或者直接后代反倒会比较麻烦。比如查找节点甲的直接父节点，你需要找到节点甲的所有祖先节点内的一个节点和节点甲之间不存在任何其他节点。对于直接子节点也类似。

select.sql
1
2
3
4
5
6
7
--- 查找评论 F 的父节点
SELECT parent.* FROM comments c JOIN comments parent 
    ON c.nlft BETWEETN parent.nlft AND parent.nrgt 
  LEFT OUTER JOIN comments in_between 
  ON c.nlft BETWEEN in_between.nlft AND in_between.nrgt 
  AND in_between.nlft BETWEEN parent.nlft AND parent.nrgt 
WHERE c.comment_id = 6 AND in_between.comment_id IS NULL;

树的维护

嵌套集结构的节点插入和移动是相当复杂的：当插入一个新的子节点时，你需要重新计算其兄弟节点、祖先节点以及祖先节点的兄弟节点，确保其左右值都要比这个新节点的 nlft 要大；当这个节点还是一个非叶子节点时，还要处理其子孙节点的左右值关系。

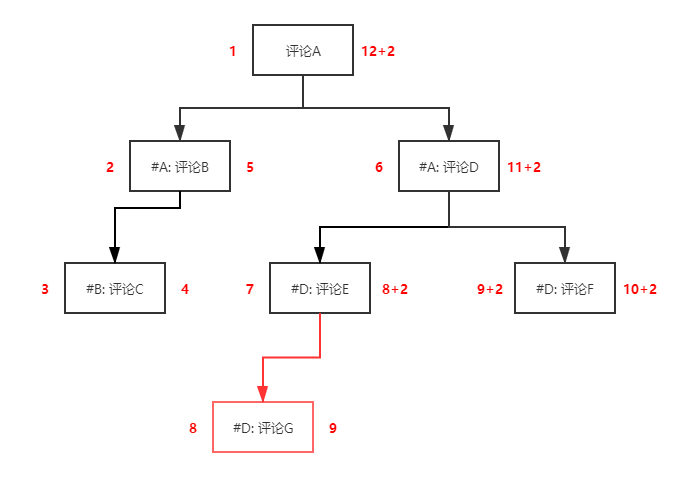
评论链条3

insert.sql
1
2
3
4
5
--- 给评论 E 新增引用评论 G 
--- 给新节点挪动空间
UPDATE comments SET nlft = CASE WHEN nlft >= 9 THEN nlft+2 ELSE nlft END, nrgt = nrgt+2 WHERE nrgt >= 8;
--- 插入新节点（左右值为 8、9）
INSERT INTO comments (comment_text, nlft, nrgt) VALUE ('G', 8, 9);

闭包表 Closure Table

闭包表是解决层级关系数据的一个简单而优雅的方案，它记录了 树中所有节点间的关系 。

我们需要另外创建一个表 comment_tree 的表，这个表只有简单的 “父-子” 关系，因此只会有两个字段 (parent - child) ，对应父子关系节点的 comment_id 。在这里，我们将每一个节点都存在一个指向自己的父子关系（针对孤立的节点），因此得到示例的表数据为。

comments

comment_id comment_text
1 A
2 B
3 C
4 D
5 E
6 F

comment_tree （由于篇幅关系，将其进行了横向排列两次）

parent child parent child
1 1 2 3
1 2 3 3
1 3 4 4
1 4 4 5
1 5 4 6
1 6 5 5
2 2 6 6

树的查询

通过 comment_tree 表，我们查找节点的祖先和后代会比嵌套集更加直观;

ancestor.sql
1
2
--- 查找评论 D 的祖先
SELECT c.* FROM comments c JOIN comment_tree t ON c.comment_id = t.parent WHERE t.child = 4;
descendants.sql
1
2
--- 查找评论 B 的后代
SELECT c.* FROM comments c JOIN comment_tree t on c.comment_id = t.cild WHERE t.parent = 2;

对于查询直接父子节点的情况，有一个优化方案就是给 comment_tree 中新增一列 path_length 表示这个父子关系的层级，自引用为 0 ，依次递增。当我们查询直接父节点或直接子节点的时候，带上查询条件 path_length=1 即可。

树的维护

对于新增一个节点，比如给评论 D 新增一个引用评论 G ：当然你首先要在 comments 中创建一条记录 (7, 'G') ，然后在 comment_tree 中创建一条自引用记录 (7, 7) ，然后再找出子节点为评论 D 即 comment_id 为 4 的节点，给他们添加一个和评论 G 的父子关系到 comment_tree 中。

要删除一个节点，需要删除 comment_tree 中以 child 为对应节点的所有记录。

delete.sql
1
2
--- 删除评论 C 
DELETE FROM comment_tree WHERE child = 3;

如果要删除的是一个子树，那么连对应节点的后代节点也要一并删除：

delete-sub-tree.sql
1
2
--- 删除评论 D 及其引用评论
DELETE FROM comment_tree WHERE child IN (SELECT child FROM comment_tree WHERE parent = 4);

注意，这里删除的仅仅是节点关系，所有的删除第一步应该是先删除 comments 表中的记录，因此要保证数据完整性你应该使用事务

移动一个节点稍微复杂一点但还是能接受，这里拿极端情况即移动一个子树而言，你需要：

  1. 断开子树和它祖先们的关系 —— 找到这个子树的顶点，删除所有子节点和它所有祖先节点间的关系；
  2. 然后将这个孤立出来的新树和新的祖先节点建立关系，这里可以用 CROSS JOIN 语句建立节点间的笛卡儿积

你需要选择哪种数据结构

这个问题问得好，这里所列举的四种范式各有优劣，所以应该根据实际的应用场景和项目需要选择适合自己的数据结构。

  • 邻接表： 直观方便、设计简单，如果你选择的数据库支持递归查询，那么臃肿的查询操作的问题也不大（当然这也考验数据库的性能）
  • 路径枚举：祖辈关系显示直观，但是使用字符串存储不仅消耗空间，同时使用 LIKE 操作效率低下，而且不能使用数据库提供引用完整性的保证，整个设计依赖于程序的正确性显得格外脆弱
  • 嵌套集：查询无递归显得非常高效，同时空间占用低，是一个非常巧妙的方案，但是相对的嵌套集的维护是这里面最为复杂的，适用于对查询有高性能需求且节点变化较小的场景
  • 闭包表：属于典型的“空间换时间”的做法，维护需要通过事务保证数据完整性，但是在查询和维护的高效和简捷上取得了一个难得的平衡。